C program to determine whether a given number is a perfect number or not

In this article, we will learn how to create a program in C that will ask the user to enter any number (at run-time) as input to check whether the given number is a perfect number or not. A perfect number is a number in which a factor's sum is equal to the number itself.

Check if the given number is a perfect number in C

The question is, "Write a program in C that checks whether a given number is a perfect number or not." The program given below is its answer. 6 is a perfect number because 1, 2, and 3 are its three factors, and after summing them up, you will get the same number itself.

#include<stdio.h>
#include<conio.h>
int main()
{
    int num, sum=0, i;
    printf("Enter any number: ");
    scanf("%d", &num);
    for(i=1; i<num; i++)
    {
        if(num%i == 0)
            sum = sum + i;
    }
    if(num == sum)
        printf("\nIt's a Perfect Number.");
    else
        printf("\nIt's not a Perfect Number.");
    getch();
    return 0;
}

The above program was built and run in the Code::Blocks IDE; here is the output. This is the first snapshot of the sample run:

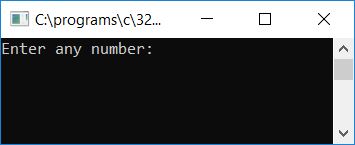
Supply any number, say 6, and press the ENTER key to see if the given number is a perfect number or not. This is the second snapshot of the sample run:

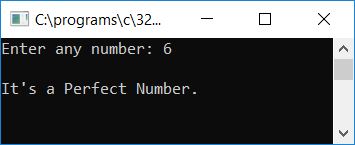
Let's check for another number, say 24. Here is the sample run for case 24 (as input):

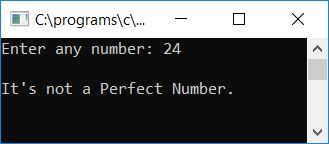
Because the factors of 24 are 1, 2, 3, 4, 6, 8, 12, finding the sum of all these factors, 1+2+3+4+6+8+12, equals 36, which is not equal to the number itself (24 here).Therefore, according to the definition of a perfect number given here, 24 is not a perfect number.

The following are some of the main steps in the above program:

• Receive any number as input, say 6.
• Make a for loop that goes from 1 to one less than the number (5 if the input is 6).
• Check whether the number is divisible by any of the numbers from 1 to one less than the number that is 5.
• If it is, then add this number to the "sum" and continue to check for the next number.
• At first run, i holds 1, and therefore the if statement evaluates like num%i == 0, or 6%1 == 0, or 0 == 0. As there will be no remainder when dividing 6 by 1, this evaluates to true, and the statement sum = sum + i or sum = 0 + 1 or sum = 1 will run inside the if block.
• Never forget to initialize the sum variable with 0 at the start of the program.
• At the second run, i is 2, and 6 is again divisible by 2 without leaving any remainder, so the statement sum = sum + i or sum = 1 + 2 or sum = 3 will run inside the if block.or 3 will be initialized to the sum variable.
• In this way, at the third, fourth, and fifth runs of the for loop, we have to process the same steps.
• At the last run, sum will have the value 6, which is equal to the number itself. Therefore,  here we have concluded that all the factors' sum of the given number, which is 6, is equal to the number itself, which is 6.
• Therefore, it is a perfect number.
• To print it out, check whether the original number is equal to the factor's sum of the given number or not.
• If it is, then print it out as a perfect number.
• Otherwise, print it out as "not a perfect number."

Print all perfect numbers in the given range in C

Here is another program on perfect numbers. This program will prompt the user to enter any two numbers as the starting and ending numbers or points, after which it will check and print all perfect numbers that exist between the given two numbers:

#include<stdio.h>
#include<conio.h>
int main()
{
    int n1, n2, i, j, sum, temp;
    printf("Enter the value of n1 (starting point): ");
    scanf("%d", &n1);
    printf("Enter the value of n2 (ending point): ");
    scanf("%d", &n2);
    printf("\nPerfect numbers between %d to %d are:\n", n1, n2);
    for(i=n1; i<=n2; i++)
    {
        temp = i;
        sum = 0;
        for(j=1; j<i; j++)
        {
            if(i%j==0)
            {
                sum = sum + j;
            }
        }
        if(temp==sum)
        {
            printf("%d\n", sum);
        }
    }
    getch();
    return 0;
}

Here is the first snapshot of the sample run:

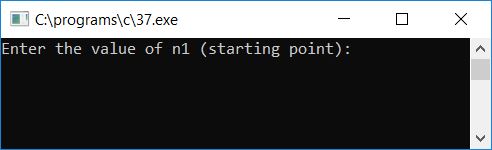
To see if the perfect number exists between any two numbers, enter 1 as the starting number and 1000 as the ending number. Here is the second snapshot of the sample run:

C Quiz