- Python Basic Programs
- Python Program Examples
- Python Print Hello World
- Python Get Input from User
- Python Add Two Numbers
- Add Subtract Multiply Divide
- Python Check Even or Odd
- Python Check Prime or Not
- Python Check Alphabet or Not
- Python Check Vowel or Not
- Python Check Leap Year or Not
- Check Reverse equal Original
- Check Positive Negative Zero
- Python Check Armstrong or Not
- Python Check Palindrome or Not
- Python Check Perfect Number
- Python Find Reverse of Number
- Python Count Digits in Number
- Python Add Digits of Number
- Sum of First and Last Digits
- Python Product of Mid Digits
- Sum of Squares of Digits
- Interchange Digits of Number
- Python Sum of n Numbers
- Python Print ASCII Values
- Python Swap Two Numbers
- Python Swap Two Variables
- Python Fahrenheit to Celsius
- Python Celsius to Fahrenheit
- Python Display Calendar
- Python Days into Years, Weeks
- Find Largest of Two Number
- Find Largest of Three Number
- Python Print Fibonacci Series
- Generate Armstrong Numbers
- Python Make Simple Calculator
- Python Add Binary Numbers
- Binary Number Multiplication
- Python Mathematical Programs
- Find Sum of Natural Numbers
- Find Average of n Numbers
- Python Print Multiplication Table
- Print Table using Recursion
- Python Find Average Percentage
- Python Find Grade of Student
- Find Square Root of Number
- Python Print Prime Numbers
- Find Numbers Divisible by
- Python Find Factors of Number
- Python Find Factorial of a Number
- Python Find HCF & LCM
- Python Kilometres to Miles
- Python Find Area of Square
- Python Find Area of Rectangle
- Python Find Area of Triangle
- Python Find Area of Circle
- Python Find Perimeter of Square
- Find Perimeter of Rectangle
- Python Find Perimeter of Triangle
- Find Circumference of Circle
- Python Simple Interest
- Python Solve Quadratic Equation
- Python Different Set of Operations
- Python Display Powers of 2
- Python Find nCr & nPr
- Python Pattern Programs
- Python Print Pattern Programs
- Python Print Diamond Pattern
- Python Print Floyd's Triangle
- Python Print Pascal's Triangle
- Python List Programs
- Python Count Even/Odd in List
- Python Positive/Negative in List
- Python Even Numbers in List
- Python Odd Numbers in List
- Python Sum of Elements in List
- Sum of Odd/Even Numbers
- Python Element at Even Position
- Python Element at Odd Position
- Python Search Element in List
- Python Largest Number in List
- Python Smallest Number in List
- Python Second Largest in List
- Python Second Smallest in List
- Python Insert Element in List
- Python Delete Element from List
- Python Multiply Numbers in List
- Swap Two Elements in List
- Python 1D Array Program
- Python Linear Search
- Python Binary Search
- Python Insertion Sort
- Python Bubble Sort
- Python Selection Sort
- Remove Duplicates from List
- Python Reverse a List
- Python Merge Two List
- Python Copy a List
- Python Conversion Programs
- Python Decimal to Binary
- Python Decimal to Octal
- Python Decimal to Hexadecimal
- Python Binary to Decimal
- Python Binary to Octal
- Python Binary to Hexadecimal
- Python Octal to Decimal
- Python Octal to Binary
- Python Octal to Hexadecimal
- Python Hexadecimal to Decimal
- Python Hexadecimal to Binary
- Python Hexadecimal to Octal
- Python Matrix Programs
- Python Add Two Matrices
- Python Subtract Two Matrices
- Python Transpose Matrix
- Python Multiply Matrices
- Python String Programs
- Python Print String
- Python Find Length of String
- Python Compare Two Strings
- Python Copy String
- Python Concatenate String
- Python Reverse a String
- Python Swap Two Strings
- Python Uppercase to Lowercase
- Python Lowercase to Uppercase
- Python Check Substring in String
- Python Count Character in String
- Count Repeated Characters
- Python Count Word in Sentence
- Python Count Each Vowels
- Python Capitalize Character
- Python Capitalize Word in String
- Python Smallest/Largest Word
- Remove Spaces from String
- Remove Duplicate Character
- Remove Vowels from String
- Remove Punctuation from String
- Python Remove Word in String
- Python Remove Duplicate Words
- WhiteSpace to Hyphens
- Replace Vowels with Character
- Replace Character in String
- Python Sort String in Alphabetical
- Sort Word in Alphabetical Order
- Extract Number from String
- Python Check Anagram Strings
- Python File Programs
- Python Read a File
- Python Write to File
- Python Append Text to File
- Python Copy Files
- Python Merge Two Files
- Python Counts Characters in File
- Python Count Words in File
- Python File Content in Reverse
- Python Lines Contains String
- Python Delete Line from File
- Python Capitalize Word in File
- Python Replace Text in File
- Replace Specific Line in File
- Python Find Size of File
- Python List Files in Directory
- Python Delete Files
- Python Misc Programs
- Python Reverse a Tuple
- Python Merge Two Dictionary
- Python bytes to String
- Python bytearray to String
- Generate Random Numbers
- Python Print Address of Variable
- Python Print Date and Time
- Python Get IP Address
- Python Shutdown/Restart PC
- Python Tutorial
- Python Tutorial
Python Program to Find Union Intersection Symmetric Difference of Sets
This article is created to cover some programs in Python, that find and prints union, intersection, difference, symmetric difference of two sets entered by user at run time. Here are the list of programs:
- Find Union of Sets
- Find Intersection of Sets
- Find Difference of Sets
- Find Symmetric Difference of Sets
Find Union of Sets
Union of two sets (A and B) can be calculated as, all elements from both the set without repeating any element.
print("Enter 5 Elements for Set A: ") setOne = [] for i in range(5): setOne.append(input()) setOne = set(setOne) print("Enter 5 Elements for Set B: ") setTwo = [] for i in range(5): setTwo.append(input()) setTwo = set(setTwo) print("\nUnion of Two Sets A and B are:") print(setOne | setTwo)
Here is the initial output produced by this Python program:
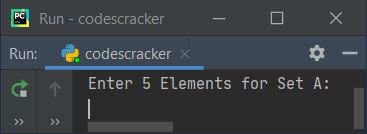
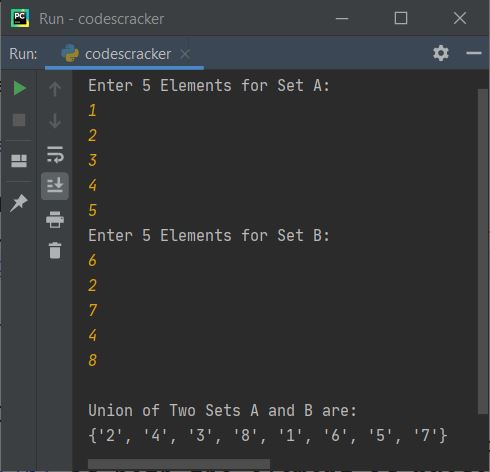
Now supply any five elements for first set (Set A) say 1, 2, 3, 4, 5 and then five more elements for second set (Set B) say 6, 2, 7, 4, 8. Then program produces the output that shows the union of two given sets like shown in the snapshot given below:
Modified Version of Previous Program
This is the modified version of previous program. This program allows user to define the size of both set along with its elements. The end= skips inserting an automatic newline.
print("Enter Size of Set A: ", end="") try: tota = int(input()) print("Enter", tota, "Elements: ", end="") numsOne = [] for i in range(tota): numsOne.append(input()) setOne = set(numsOne) print("\nEnter Size of Set B: ", end="") try: totb = int(input()) print("Enter", totb, "Elements: ", end="") numsTwo = [] for i in range(totb): numsTwo.append(input()) setTwo = set(numsTwo) unionSet = setOne | setTwo print("\nSet A: ", "{", ', '.join(setOne), "}") print("Set B: ", "{", ', '.join(setTwo), "}") print("\nUnion of A and B =", "{", ', '.join(unionSet), "}") except ValueError: print("\nInvalid Input!") except ValueError: print("\nInvalid Input!")
Here is its sample run with user input 3 as size of first set (set A), then 1, 2, 3 as three elements, and 4 as size of second set (set B), then 1, 2, 3, 4 as its four elements:
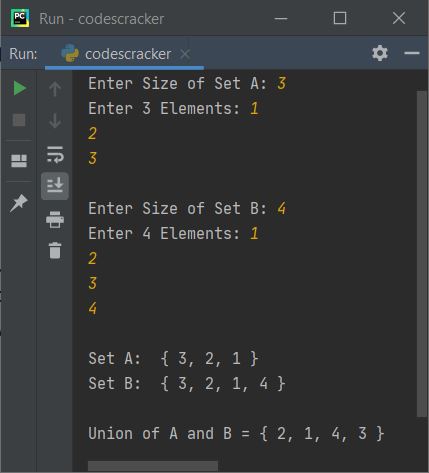
Note - The join() in above program is used in a way, to remove ' from all elements of set.
Find Intersection of Sets
Intersection of two sets (A and B) can be calculated as, all common elements from both the set.
To create a Python program that finds intersection of sets given by user at run-time just like the previous program that finds union. Follow the previous program with only two replacements. That is, first replace the following statement (from previous program):
unionSet = setOne | setTwo
with the statement given below:
intersectionSet = setOne & setTwo
And then replace the following (second) statement (from above program):
print("\nUnion of A and B =", "{", ', '.join(unionSet), "}")
with the statement given below:
print("\nIntersection of A and B =", "{", ', '.join(intersectionSet), "}")
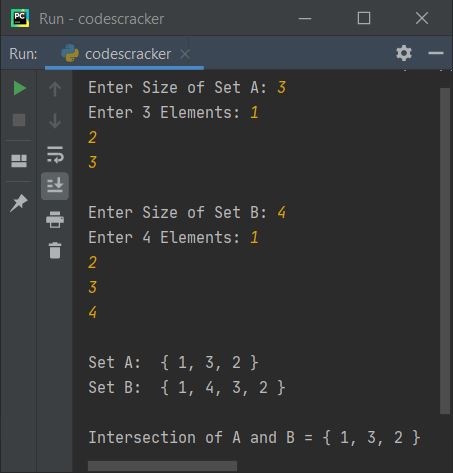
Now here is its sample run with same user input as of previous program's sample run:
Find Difference of Sets
Difference of two sets (A and B) can be calculated as, all those elements that are present in set A but not in set B
To find difference of sets in Python, do the similar thing as done previously. That is, change the following two statements from the program given in modified version of union of set program. That is, replace the following statement:
unionSet = setOne | setTwo
with:
diffSet = setOne - setTwo
and then replace the second statement, that is:
print("\nUnion of A and B =", "{", ', '.join(unionSet), "}")
with:
print("\nDifference of A and B =", "{", ', '.join(diffSet), "}")
Here is its sample with user input, 5 as size of first set, then 1, 2, 3, 4, 5 as its five elements and 2 as size of second set, then 1, 6 as its two elements:
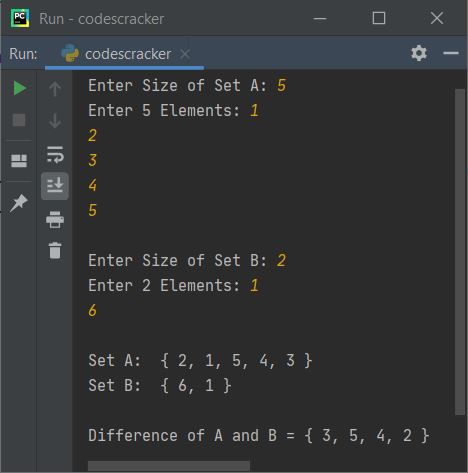
Find Symmetric Difference of Sets
Symmetric difference of two sets (A and B) can be calculated as, all unique elements from both the set.
Like done previously, in this case also, change the two statements with following two statements one by one:
symDiffSet = setOne ^ setTwo print("\nSymmetric Difference of A and B =", "{", ', '.join(symDiffSet), "}")
Here is its sample run with user inputs 4 as size of set A, then 5, 6, 7, 8 as its four elements, and 3 as size of set B, then 1, 2, 7 as its three elements:
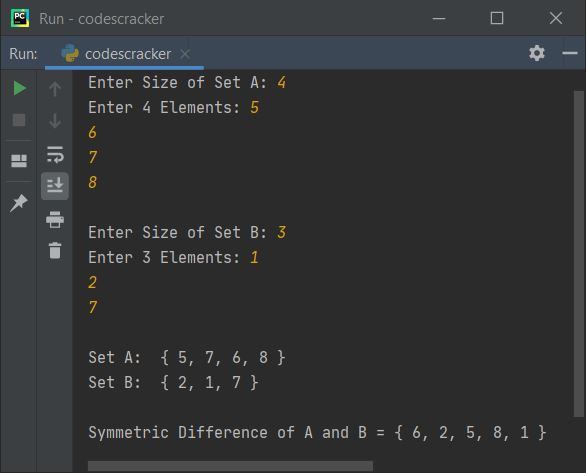
Find all Four Operations on Two Sets
This program is the combine version of previous four programs, that find and prints all the four operations of two given sets.
print("Enter Size of Set A: ", end="") try: tota = int(input()) print("Enter", tota, "Elements: ", end="") numsOne = [] for i in range(tota): numsOne.append(input()) setOne = set(numsOne) print("\nEnter Size of Set B: ", end="") try: totb = int(input()) print("Enter", totb, "Elements: ", end="") numsTwo = [] for i in range(totb): numsTwo.append(input()) setTwo = set(numsTwo) unionSet = setOne | setTwo intersectionSet = setOne amp; setTwo diffSet = setOne - setTwo symDiffSet = setOne ^ setTwo print("\nSet A: ", "{", ', '.join(setOne), "}") print("Set B: ", "{", ', '.join(setTwo), "}") print("\nUnion of A and B =", "{", ', '.join(unionSet), "}") print("\nIntersection of A and B =", "{", ', '.join(intersectionSet), "}") print("\nDifference of A and B =", "{", ', '.join(diffSet), "}") print("\nSymmetric Difference of A and B =", "{", ', '.join(symDiffSet), "}") except ValueError: print("\nInvalid Input!") except ValueError: print("\nInvalid Input!")
Here is its sample run:
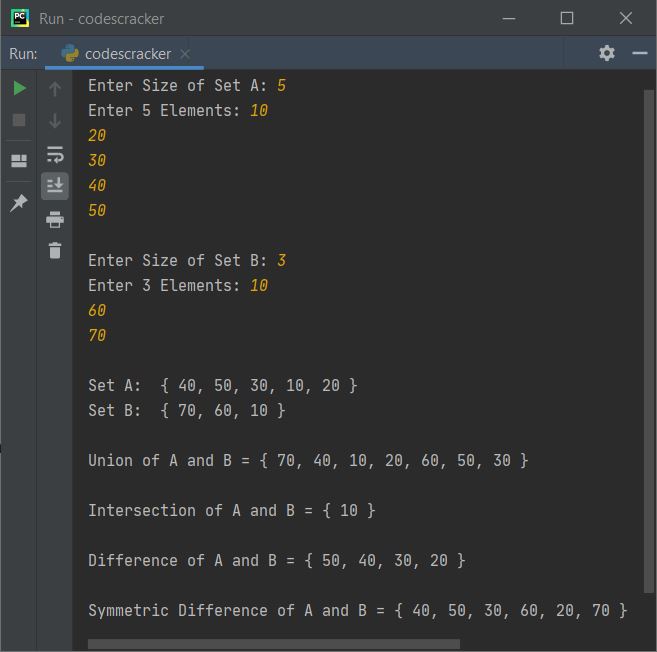
« Previous Program Next Program »