- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
Binary to Hexadecimal Conversion Steps, Formula, and Example
In the event that we need to convert a number from binary to hexadecimal, this article, which was created and published, will walk us through the necessary steps and formula, as well as provide an example.
However, before we move on to the steps, formula, and example of converting binary to hexadecimal, we need to take a quick look at these two numbers. So, what exactly are we holding out for? Let's talk quickly about these two numbers, shall we?
- Binary numbers: Because 0 and 1 are the only two digits that can be used, binary numbers are the only ones that can be produced using
those two digits alone. To put it another way, we can say that a number that consists of nothing but the digits 0 and 1 is what is known as a
binary number. This is because binary numbers can only contain these two digits. The numbers 1101, 111011, and 1010111 are a few examples among
many others.
Keep in mind that binary numbers have a base of 2, which indicates that a binary number is comprised of a total of two digits, which are the digits 0 and 1. This is an additional fact regarding binary numbers that should be kept in mind. - Hexadecimal number: On the other hand, a hexadecimal number can have any of the 16 possible digits because its base is 16. These digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. Take, for instance, the numbers 23D, AF, and 32DF, etc. It is necessary to specify the base of a number before we can use it to represent it in hexadecimal. Take, for instance: (23)16.
Binary to Hexadecimal Steps
In order to convert any number from the binary number system to the hexadecimal number system, we need to follow these steps in the correct order:
- The digits of the binary number should be separated into four pairs each.
- When creating a pair of 4-bit numbers, start with the least significant bit (LSB) and work your way up to the most significant bit (MSB).
- Converting each 4-bit binary number to its corresponding hexadecimal value is the next step.
- Now add up all of the numbers that have been converted; this will result in the same number, but expressed using the hexadecimal number system.
Binary to Hexadecimal Formula
Here are the rules that help you convert any given binary number into its equivalent hexadecimal value: Let's suppose that the user has entered 1101110 as a binary number input.
- Then we have to first make 4-4 pairs of the given binary digits from the right side, that is, 1101110 has a total of 2 pairs of 4-4 digits from the right side.
- That is, the first pair will be 1110, and the second pair will be 110.
- You can add 0 at the beginning of the second binary pair to make it a 4-digit pair.
- That is after inserting a 0 at the start of the binary pair 110.
- The pair is renamed 0110.
Now convert each of the two binary pairs into the hexadecimal value that corresponds to it, as shown in the two boxes given below:
23 22 21 20
8 4 2 1
0 1 1 0 (last or second binary pair)
4 2 (write below 1 only)
=4+2 (sum up all values)
=6
The first binary pair's value has been converted into its corresponding hexadecimal value, which is as follows:
23 22 21 20 8 4 2 1 1 1 1 0 (last or second binary pair) 8 4 2 (write below 1 only) =8+4+2 (sum up all values) =14
Now we have two hexadecimal digits, which are 6 and 14, and we've already told you that digits 10 to 15 must be replaced with characters ranging from A to F. As a result, 6 will remain unchanged, and 14 will be converted with E. That is, 6E is the final hexadecimal value of a given binary number 1101110. Therefore, (1101110)2 = (6E)16.
Binary to Hexadecimal Example
Let's take an example to see how we can convert a binary number to a hexadecimal number.
We have a number, say, 1010111110110010; now we have to convert it into hexadecimal form. See the figure given below:
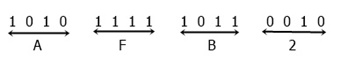
As you can see from the above figure, we have a total of 4 digits, which are A, F, B, and 2. Now combine all the four digits, we will get AFB2, which is the same number but in hexadecimal form.
Therefore, (1010111110110010)2 = (AFB2)16
Programs Created on Binary to Hexadecimal Conversion
- Binary to Hexadecimal in C
- Binary to Hexadecimal in C++
- Binary to Hexadecimal in Java
- Binary to Hexadecimal in Python
« Previous Tutorial Next Tutorial »