Decimal to Hexadecimal Conversion with Examples

This post, which was created and published, explains the method that is utilized when converting a number from the decimal number system to the hexadecimal number system. The explanation is accompanied by an example. But before we get started, let's first go ahead and define these two different number systems.

Decimal number: The decimal number system has a base of 10, therefore it allows 10 digits, which are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, to form a decimal number. For example: 123034, 40, and 984, etc.
That is, any number that is made up of these 10 digits can be considered a decimal number.
Hexadecimal number: On the other hand, the hexadecimal number system has a base of 16, which means this number system allows a total of 16 digits to form a hexadecimal number. Those 16 digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. Some examples of hexadecimal numbers are 13D, F340, and FA, etc.
The symbols A, B, C, D, E, and F are the single-digit representations of 10, 11, 12, 13, 14, and 15.

Decimal to Hexadecimal Conversion Steps

Follow the steps below to convert a number in the decimal number system to its hexadecimal equivalent:

To begin, divide the decimal number by 16 and save the remainder.
Continue dividing the decimal number by 16 until you reach a quotient value of zero.
Take all of the remainder values and write them backwards to get the hexadecimal equivalent.
Finally, remember to replace 10, 11, 12, 13, 14, and 15 with A, B, C, D, E, and F.

In order to make things easier for you, I have compiled a table below that lists all of the hexadecimal equivalents of decimal digits:

Decimal	Hexadecimal Equivalent
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	A
11	B
12	C
13	D
14	E
15	F

To help you understand the conversion in the most effective way possible, I believe that it is the appropriate time for you to look at an example at this point. So, what exactly are we holding out for?
Take this example as a way to illustrate how much simpler things can be for you.

(259)₁₀ = ( ? )₁₆.

We have a number written in decimal notation, which is 259. Now we must figure out what that number's representation is in hexadecimal. Take a look at the following conversion figure, which explains everything by using the figure itself as an example.

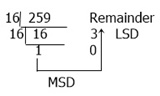
From the above figure, we have the value 103 in the hexadecimal system, which is the same number. Therefore, (259)₁₀ = (103)₁₆.

Allow me to provide another example. I'm going to convert the decimal number 843 to its hexadecimal equivalent for this.

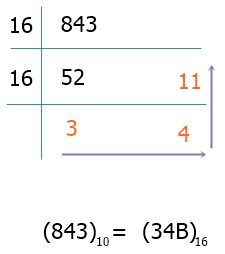
To represent 11 in hexadecimal, we need to use B; therefore, I have written B in place of the remainder 11.

Programs Created on Decimal to Hexadecimal Conversion

Computer Fundamentals Quiz

« Previous Tutorial Next Tutorial »

Liked this post? Share it!