- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
Bitwise Operators with Example
Bitwise operators are used for bitwise manipulation. That is, bitwise operators operate on binary integers and units. That is, whatever the operand value is, the bitwise operator performs the calculation on its binary equivalent's values.
Types of Bitwise Operators
These are the six types of bitwise operators:
- Bitwise AND (&)
- Bitwise OR (|)
- Bitwise XOR (^)
- Bitwise NOT (˜)
- Bitwise Right Shift (>>)
- Bitwise Left Shift (<<)
Now that we've gone over all of the bitwise operators, let's go over each one in greater detail and understand it using an example that's both concise and easy to grasp.
Bitwise AND (&)
The truth table for the bitwise AND or bitwise & operator is as follows:
| A | B | A & B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
For example:
0011 1100 (60) & 0000 1101 (13) ----------- 0000 1100 (12)
Therefore, 60 & 13 = 12.
Bitwise OR (|)
The truth table for the Bitwise OR or Bitwise | operator is as follows:
| A | B | A | B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
For example:
0011 1100 (60) | 0000 1101 (13) ----------- 0011 1101 (61)
Therefore, 60 | 13 = 61.
Bitwise XOR (^)
The truth table for the Bitwise XOR or Bitwise ^ (also known as Bitwise Exclusive OR) is as follows:
| A | B | A ^ B |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
0011 1100 (60) ^ 0000 1101 (13) ----------- 0011 0001 (49)
Therefore, 60 ^ 13 = 49.
Bitwise Not (˜)
The Bitwise NOT or Bitwise ˜ operator, unlike other Bitwise operators, is an unary operator.A unary operator is one that only operates on one operand or takes one input.
The bitwise NOT operator complements each bit of input one by one. We can understand "complement" here as reverse. The following is the truth table for the Bitwise, NOT operator:
| A | ˜A |
|---|---|
| 1 | 0 |
| 0 | 1 |
For example:
˜ 0111 (7) ------ 1000 (8)
Therefore, ˜7 = 8.
Bitwise Right Shift (>>)
The Bitwise Right Shift, or Bitwise >> operator, shifts the binary sequence to the right. For example, the binary equivalent of 14 is 0000 1110 (8-bit binary equivalent), and then 14 >> 1 gives 000 0111. The graphic representation of the Bitwise right-shift operation is shown below:
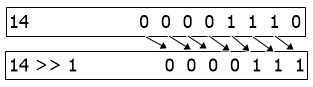
Note: Empty places get replaced by 0. As a result, 14 >> 1 = 0000 0111 (which 7).
Similarly, 14 >> 2 can be calculated as:
14 0000 1110 14 >> 2 00 0011
Therefore, 14 >> 2 = 0000 0011 (which equals 3). That is, the binary equivalent of 14 is shifted two bits to the right.
Bitwise Left Shift (<<)
The Bitwise Left Shift, or Bitwise << operator, shifts the binary sequence to the left. For example, the binary equivalent of 14 is 0000 1110 (8-bit binary equivalent), and then 14 << 1 gives 0001 1100. The figure given below shows, in graphical form, how the bitwise left shift operation performs:
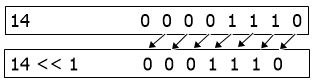
Note: In bitwise left shift, empty places also get replaced by 0. Therefore, 14 << 1 = 0001 1100 (that is equal to 28).
Similarly, 14 << 2 can be calculated as:
14 0000 1110 14 << 2 0011 10
Therefore, 14 << 2 = 0011 1000 (that is equal to 56).
« Previous Tutorial Next Tutorial »