- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
Decimal to Octal Conversion with an Example
This entire post will be devoted to the topic of "converting from decimal to octal." In other words, by reading this article, you will gain an understanding of the process that is used to convert a number from the decimal number system to the octal number system equivalent of that number. But before we get started, I believe it is important for us to first grasp these two numerical values. Let's begin by defining these two different number systems.
- Decimal number: Decimal numbers are those that are made up of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. For example: 439, 908,
23, etc.
One more thing regarding decimal numbers that you need to keep in mind is that they have a base of 10, as shown here. When a number is expressed using the base 10 system, it has a total of 10 digits to represent it. These ten digits range from zero to nine. - Octal number: On the other hand, the octal number system has a base of 8, which means it allows eight digits, which are 0, 1, 2, 3, 4, 5, 6, and 7. For example, 437, 32, and 506, etc. are some examples of octal numbers.
Decimal to Octal Steps and Example
In order to convert a number from decimal to octal, we must divide the decimal number by 8, as this is the base of the octal number system. Let's look at an example of this so that we can get a better grasp on it.
(204)10 = ( ? )8.
Converting the decimal representation of the number 204 to the octal system is required, as demonstrated by the preceding illustration.
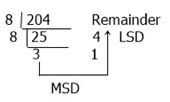
Look at the above figure carefully. We first divided the number 204 by 8, yielding 25 as a result and 4 as a remainder; now divide 25 by 8. Continue dividing until the number becomes less than the number through which you are dividing, which is 8 here.
Always write the remainder on the right side of the result. After dividing the number or after getting a remainder less than 8, stop dividing and write the remainder from last to first. Here we have 314 as the result, or octal value, of the same number given in decimal, that is, 204. Therefore, (204)10 = (314)8.
Another Example of Decimal to Octal
Let me give another example by converting the decimal number 843 into its octal equivalent.
843 % 8 (which results in 105 as the quotient and 3 as the remainder) 105 % 8 (which gives a quotient of 13 and a remainder of 1) 13 % 8 (gives a quotient of 1 and a remainder of 5)
Include the last quotient and write all the remainder digits from the last to the first, yielding 1513. As a result, (843)10 = (1513)8.
Programs Created on Decimal to Octal Conversion
« Previous Tutorial Next Tutorial »