- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
Octal to Hexadecimal Conversion Steps and Examples
This post was written and distributed with the intention of elaborating on the processes that can be applied in order to convert a number written in the octal number system to the hexadecimal number system. But before we get started, let's first discuss what these two numbers mean.
- Octal number: The octal number system has a base of 8, which means this system allows 8 digits to be used to form an octal number. Those 8 digits are 0, 1, 2, 3, 4, 5, 6, 7. For example: 213, 73, and 3023, etc.
- Hexadecimal number: On the other hand, the hexadecimal number system has a base of 16, which means this system allows 16 symbols to be
used to form a hexadecimal number. Those 16 symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. For example: 33DA, 304, and 9AF, etc.
Let me clarify one more thing about hexadecimal numbers: here I used a symbol instead of a digit because of A-F. Because the decimal values 10, 11, 12, 13, 14, and 15 are represented by A, B, C, D, E, and F in this number system.
Octal to Hexadecimal Formula
To convert any octal number to the hexadecimal system, we must first convert the octal number to binary, and then the binary number to hexadecimal.
For example, (435)8 = ( ? )16
We have to convert the above number, 435, given in the octal system, into the hexadecimal number system. then we have to convert its binary equivalent. The figure given below shows its binary equivalent, or the binary equivalent of 435.
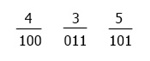
According to the figure given above, we have 100 011 101 as the value, which is the binary equivalent of the octal number 435. Now let's convert it into the hexadecimal system. Or we have to calculate: (100011010)2 = ( ? )16
Before proceeding, we have to make 4-4 pairs of binary bits, and here we have a total of 9 digits; therefore, to make 4-4 pairs, we have to add 3 zeros before the number; after adding three zeros, we have 000100011101. Now make 4 pairs and convert each pair into its hexadecimal equivalent, as shown in the figure given below.
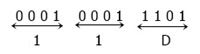
According to the above figure, the hexadecimal equivalent is 11D. Therefore, (435)8 = (11D)16.
Octal to Hexadecimal Steps
Let's say the octal number that has been provided to us is 1452. Now that you've got that out of the way, give the information contained in the following box your full attention:
1 4 5 2 (write all octal digits) 001 100 101 010 (write its binary equivalent) 001100101010 (combine all binary digits) 0011 0010 1010 (make a 4-4 binary pair) 3 2 10 (write the decimal equivalent of each binary pair) 3 2 A (convert digits 10 to 15 into characters A to F) = 32A
As you can see from the above box:
- First, you have to write all the octal digits.
- And then write the binary equivalent of each octal digit one by one in a 3-3 binary pair.
- Then combine all the binary pairs. Now make 4-4 binary pairs.
- Write the decimal equivalent of each binary pair.
If any digit greater than 9 is available as a decimal digit, then convert it into a character as told above. Therefore, from the above box, the hexadecimal equivalent of the given octal number 1452 is 32A. You can also write (1452)8 = (32A)16.
Programs Created on Octal to Hexadecimal Conversion
- Octal to Hexadecimal in C
- Octal to Hexadecimal in C++
- Octal to Hexadecimal in Java
- Octal to Hexadecimal in Python
« Previous Tutorial Next Tutorial »