- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
Binary Search Logic and Algorithm with Example
This article, which was produced and published with the intention of providing a description of the logic and algorithms involved in binary search along with an example.
The Logic of Binary Search
The following is the step-by-step logic behind binary search:
- Divide the sorted array in half (lower half and upper half) by using (first index) + (last index)/2.
- Now you will get the index number (middle index) by applying this division.
- Check whether the number present at this index is equal to the number to be searched for or not.
- If it is equal, then stop searching. Print the value of that index where the number is found.
- And if it is not, then check whether the given number is greater than or less than the number present at the middle index or not.
- If it is greater than the number present at the middle index, then skip the lower half and process for the upper half using the same logic as used in the first step. Except replace the first index's value with middle+1.That is, middle+1 replaces the value of the first index.
- And if it is less than the number present at the middle index, then skip the upper half and process for the lower half using the same logic as used in the first step. Except, put the value of last index with middle-1. That is, middle-1 replaces the value of the last index.
- Continue checking until the value is found or the interval becomes zero.
- If the value is found, print the index number as the position of the given number. Otherwise, if interval becomes zero, then print as the number is not found in the array.
Important Reminder
Before beginning the binary search, you must first sort the array that has been provided to you. This is the most important factor to keep in mind. To sort an array, you can use any method, including the following:
After the array has been sorted, you may perform a binary search on it.
Binary Search Algorithm
You will have a solid grasp of the algorithm for the binary search if you have a solid comprehension of the logic that is used behind the binary search as mentioned above. The following is the algorithm for performing a binary search:
- Find the middle index using (first+last)/2.
- If the element at the middle index equals a number, print the middle index.
- If the element at the middle index is greater than the number, (last) = (middle index) - 1. Go to the first step.
- If the element at the middle index is greater than the number, (first) = (middle index) + 1. Go the the first step.
- Continue until the second step gets evaluated or the middle index becomes zero.
- Print "Number not found" if the middle index becomes zero.
Binary Search Example
Utilizing the binary search strategy, one could, for instance, look for the element 46 in the list that consists of 4, 10, 16, 24, 32, 46, 76, 112, 144, and 182. Using this example, let's take a look at the following figure, which provides a lot of information regarding binary search:
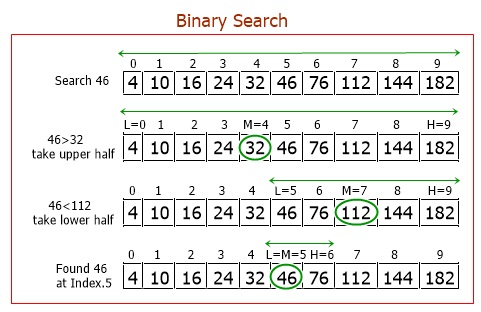
Therefore, 46 is found at index number 5.
Programs Created Using Binary Search
« Previous Tutorial Next Tutorial »