- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
Binary Number Addition Rules and Examples
This document has been written and made public with the intention of elaborating on the procedures that are followed when doing binary addition or when adding two binary values.
Binary numbers are simply numbers that only contain the digits 0 and 1. Because the binary number system only permits the use of the numbers 0 and 1, there is no room for any other numbers.
Data saved in a computer, as we all know, is a series of binary digits, i.e., 0 and 1. The sequence now important since it is understood differently depending on how it is used.
Essentially, the binary sequence encodes computer instructions, and the data types vary depending on the conditions.
In binary, information is stored using either bits or bytes. A bit is the most fundamental unit of data. It indicates a logical state with one of two potential values: 0 or 1. In the case of bits, the only two numbers utilized are 0 and 1. As an example: 1. A byte is a type of unit, however it is not the most fundamental. It is a type of information unit that typically consists of eight bits. A byte is the smallest addressable unit of memory in various computer architectures. For instance, 10010101
A "bitstream" is a binary sequence with a bit sequence. A "bytestream" is a binary sequence that contains a series of bytes.
Now that we've covered the basics, let's get into the meat of the matter: the rules and examples for adding two binary numbers.
Rules for Performing Addition on Binary Numbers
When executing the operation of adding two binary values, these are the considerations that need to be kept in mind at all times.
- 0+0 gives 0
- 1+0 gives 1
- 0+1 gives 1
- 1+1 gives 0 with 1 as carry
- 1+10 gives 1 with 1 as carry
11 is equal to 1 plus 10 or 10 plus 1, or 1 with a carry of 1.
Example of Addition for Binary Numbers
Let's look at an example to better illustrate what I mean:
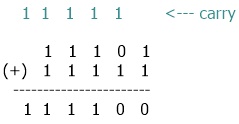
1 1 1 0 1 + 1 1 1 1 1 -------------- 1 1 1 1 0 0
Here is the list of all steps performed in the above addition of two binary numbers:
- The addition always goes from right to left. Therefore
- Initially, 1 + 1 equals 0 with 1 as the carry.
- At second, 0+1 gives 1, and 1+1 (carry) gives 0, with 1 as carry again.
- At third, 1+1+1 (carry) is equal to 11, which gives 1 with 1 as carry.
- At fourth, 1+1+1 (carry) is equal to 11, which gives 1 with 1 as carry.
- At fifth, 1+1+1 (carry) gives 11 again.
- Now, from bottom to top, take all values after giving.
- We get 111100.
- Therefore, 11101 + 11111 = 111100.
Pictorial Representation of Binary Addition
You should no longer have any questions about binary addition after looking at the diagram. The example that is drawn from the picture that follows, which adds together two binary values, is the ideal one to use in order to comprehend the addition rule in its entirety:
« Previous Tutorial Next Tutorial »