Number System and its Types

This article was written with the intention of elaborating on the various kinds of number systems. In addition to that, I penned a total of twelve articles, each of which provides an explanation of the process by which numbers can be converted from one number system to another. And for your convenience, the links to each of those 12 required articles are provided at the bottom of this article. This way, you can easily access any of the articles if you so choose. Now that we have that out of the way, let's begin by defining "number system."

Definition of Number System

A set of values that can be used to represent quantity is defined by a number system.

The number system is a language of digital systems consisting of a set of symbols called digits with rules defined for addition, multiplication, and other mathematical operations.

The base, or radix, of a number system is the number of symbols used in its representation.

Types of Number Systems

There are four types of number systems in general, which are listed below.

Decimal number system
Binary number system
Octal number system
Hexadecimal number system

Now, let's move on to providing a concise explanation of each of these four varieties of number systems, beginning with the "decimal number system."

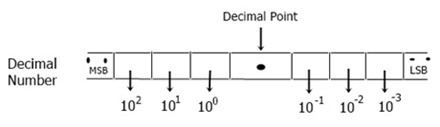
Decimal Number System

The decimal number system is also called the "base-10 system" because it has a total of 10 digits to use that are from 0 to 9.

Binary Number System

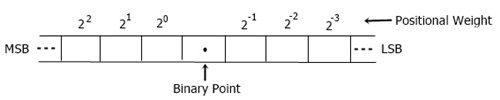
From the standpoint of a computer, the binary number system is the most important and valuable of all number systems. As we all know, a computer cannot operate on the decimal system or any other number system because it only operates using binary logic.

This number system only uses two digits or symbols, that is, 0 and 1. Alternatively, we can state that this system will only rely on and operate on a 0 and 1 basis.

Octal Number System

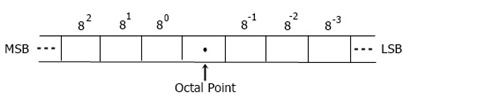
The octal number system uses digits from 0 to 7, for a total of 8 digits or symbols.

Hexadecimal Number System

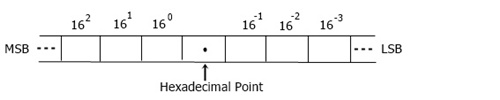
This number system uses 16 digits or symbols. In 16 digits, 10 digits are from 0 to 9, and the other 6 are from A to F.

All Number System Bases

The following table provides a list of all four different number systems, along with the bases or radixes for each system.

Number System	Base
Binary	2
Octal	8
Decimal	10
Hexadecimal	16

Symbols Used in All Four Number Systems

The decimal number system uses 10 symbols, which are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

The binary number system uses only two symbols, which are 0 and 1.

The octal number system uses 8 symbols, which are 0, 1, 2, 3, 4, 5, 6, and 7.

The hexadecimal number system uses 16 symbols, which are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. A–F are single-bit representations of decimal values 10–15. That is, A refers to 10, B refers to 11, C refers to 12, D refers to 13, E refers to 14, and F refers to 15.

Number System Conversion

I am not going to go into detail about how to convert numbers from one number system to another within the scope of this article because the process is covered in greater depth within other guides. However, if you are interested in understanding the processes and algorithms that are utilized in the process of converting one number from one number system to another, the following is a list of articles that you might find it helpful to read.

Computer Fundamentals Quiz

« Previous Tutorial Next Tutorial »

Liked this post? Share it!