Binary to Octal Conversion with Example

This article was created and published to describe the way to convert a number from binary to octal, along with an example. But before we begin, let's define the binary and octal numbers first.

• Binary number: The binary number system has a base of 2, which means it allows two digits, which are 0 and 1, to form a binary number. For example, 1101, 111011, and 111, etc.
  That is, any number that contains 0 and 1 can be called a binary number.
• Octal number: On the other hand, the octal number system has a base of 8, which means it allows eight digits, which are 0, 1, 2, 3, 4, 5, 6, and 7. For example, 2350, 35, and 203, etc. are some examples of octal numbers.

Binary to Octal Conversion Methods

We have two methods to convert any binary number to octal.

• Convert Binary to Decimal, then Decimal to Octal
• Convert directly from binary to octal

Only the second approach will be covered in this article. Because we have already talked about both of the conversions when we were discussing the first method. You can refresh your memory by following the individual tutorials for each of these two.

Binary to Octal Conversion Steps

Follow all the steps given below for the binary to octal conversion:

1. Group the binary bit into a group of 3 parts, starting from the LSB.
2. Place 1 or 2 0s as required before binary numbers if the total number of digits is not divisible by 3. As we have to make pairs of 3–3 digits, what if we have 8 digits like 10110100, 8 is not divisible by 3, we have to append 0 before 10110100 to make it 010110100.
3. Now convert each group to its equivalent decimal.

Binary to Octal Conversion Formula

Here are the rules that help in the conversion of binary to octal:

• Let's suppose the given binary number is 1101110.
• We have to convert it into its equivalent octal value.
• Then we must first create three pairs of binary digits from the right side.
• As a result, the 3-3 pair of 1101110 from the right side will be 110 (first pair), 101 (second pair), and 1 (third pair).
• You can add zero (0) at the beginning of the third pair; that becomes 001 after adding two zeros at the beginning of the third pair.
• We must now convert each pair into its equivalent octal value one by one.

Here is the conversion of the third binary pair, 001, into its equivalent octal value:

22  21  20
4   2   1

0   0   1   (last binary pair)
        1   (write below 1 only)
= 1         (add up all the values)

Here is the conversion of the second binary pair, 101, into its equivalent octal value:

22  21  20
4   2   1

1   0   1   (second binary pair)
4       1   (write below 1 only)
= 4 + 1     (add up all the values)
= 5

Here is the conversion of the first binary pair, 110, into its equivalent octal value:

22  21  20
4   2   1

1   1   0   (first binary pair)
4   2       (write below 1 only)
= 4 + 2     (add up all the values)
= 6

Now we have three octal digits, which are 1, 5, and 6. Therefore, the octal value of 1101110 is 156.

Binary to Octal Conversion Example

Now let's take an example of how to convert the number 11010010 in binary form to the octal number system.

Or, convert (11010010)₂ = (?)₈.

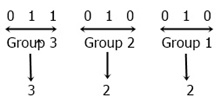
As you can see from the above figure, after converting the number 11010010 given in binary form into the octal number system, we get 322.

Therefore, (11010010)₂ = (322)₈.

Programs Created on Binary to Octal Conversion

• Binary to Octal in C
• Binary to Octal in C++
• Binary to Octal in Java
• Binary to Octal in Python

Computer Fundamentals Quiz