Pascal's Triangle

In this article, you will get a brief description of Pascal's triangle. Here, the simplest description of Pascal's triangle is given. I'm not going into detail about it. Because the purpose of this article is only to provide an idea to every programmer on this site so that they can easily create a program on it.

How Pascal's Triangle Expands

Here is the algorithm to create a Pascal's triangle. These steps can be used to create it in any of your favorite languages, such as C, C++, Java, Python, etc.

There is only one column in the first row with a value of 1.
The value of the first and last column for every row is 1.
In the second row, there are two columns. So the addition of both columns gets placed as the value of the second column of the next (third) row.
In the third row, there are three columns. So the addition of the first and second columns gets placed as the value of the second column of the next (fourth) row. Again, the addition of the second and third columns gets placed as the value of the third column of the next (fourth) row.
In the fourth row, there are four columns. So the addition of the first and second columns gets placed as the value of the second column of the next (fifth) row. Again, the addition of the second and third columns gets placed as the value of the third column of the next (fifth) row. Again, the addition of the third and fourth columns gets placed as the value of the fourth column of the next (fifth) row.
If there are more rows, repeat the process.

Structure of Pascal's Triangle

Pascal's triangle is like an equilateral triangle. In it, there are:

only one column in the first row
2 columns in the second row
3 columns in the third row
and so on.

where every next row is created in a way that

The value of the second column is the sum of the first and second columns of the previous row.
The value of the third column is the sum of the previous row's second and third columns.
The value of the fourth column is the sum of the previous row's third and fourth columns.
and so on.

Now let's see the pictorial representation of Pascal's triangle.

Pascal's Triangle Formula

Here is a simple formula to find the column value of every row of a Pascal's triangle.

value = (row!)/((column!)*(row-columns)!)

The ! indicates factorial. Both the row and column begin at 0. That is, to determine the value of the second column of the fourth row. As a result of entering the row and column values, we get:

value = (row!)/((column!)*(row-columns)!)
      = (4!)/((2!)*(4-2)!)
      = (24)/(2*(2!))
      = 24/(2*2)
      = 24/4
      = 6

So 6 is the number present in the fourth row and second column. The factorization of a number n is calculated as:

n! = n*(n-1)(n-2)*(n-3)*....*1

So the factorial of 4 is:

4! = 4*3*2*1
   = 24

Pictorial Representation of Pascal's Triangle

Here is the step-by-step pictorial representation of a Pascal's triangle that is composed of 5 rows. Here is the first one:

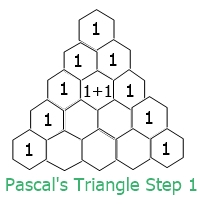
This is the second one.

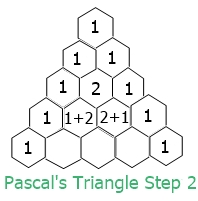
Below is the third one:

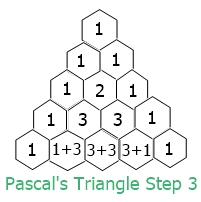
And here is the final one:

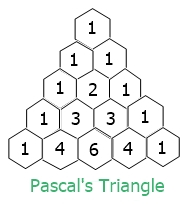
To learn more about it, you can Google it. But the required knowledge about Pascal's triangle is given. You can now proceed to the programming stage and create it in any programming language of your choice.

Programs Created on Pascal's Triangle

« Previous Topic Next Topic »

Liked this post? Share it!