- Mathematics and Other
- Find LCM
- Find HCF
- Matrix Addition
- Matrix Subtraction
- Matrix Multiplication
- Triangle Area and Circumference
- Celsius to Fahrenheit
- Pascal's Triangle
- Explanation of Leap Year
- Computer Programming
- Learn Python
- Python Keywords
- Python Built-in Functions
- Python Examples
- Learn C++
- C++ Examples
- Learn C
- C Examples
- Learn Java
- Java Examples
- Learn C#
- Learn Objective-C
- Web Development
- Learn HTML
- Learn CSS
- Learn JavaScript
- JavaScript Examples
- Learn SQL
- Learn PHP
How to Find LCM
You will learn how to calculate the least common multiple (LCM) of two or more numbers by reading this article. But before we get into the formula or method for calculating the least common multiple of a set of numbers, let's first get a grasp on what LCM is.
What is LCM?
LCM stands for "Least Common Multiple." It is used to find the smallest positive integer that is divisible by all the numbers (from which the LCM is computed). For example, the LCM of 2 and 3 is 6, as indicated by:
LCM(2, 3) = 6
As you can see, the number 6 is divisible by both the numbers 2 and 3. LCM (Least Common Multiple) can also be called:
- Lowest Common Multiple
- Least Common Divisor
Both expressions mean the same thing, which is to locate the smallest number such that it can be divided by the numbers that are provided (to which the LCM is to be calculated).
However, there is another method we can approach to find the LCM of a given set of numbers. Let's discuss.
Methods to find LCM
To find LCM, there are multiple methods available. But here, we will only discuss two popular methods:
Listing Multiples Method
To find LCM using the listing multiples method, we have to follow the algorithm given below:
- Write down the multiple of all the given numbers.
- Find the smallest number that is available in every number's multiples.
- That smallest number will be the LCM.
Multiples of a number are numbers that are the products of a given number. For example, multiples of 3 are 3, 6, 9, 12, 15, 18, and so on. That is, when we multiply 3 by 5, we will get 15, which is the multiple of 3. Similarly, if we multiply 3 with any other number, the result we get will be the multiple of 3.
For example, let's find the LCM of 10, 12, and 15. Since I already stated that, we need to write down the multiples of these numbers and the least common multiple from all the lists of common multiples. Here is the list of some multiples of all three numbers:
- Multiples of 10: 10, 20, 30, 40, 50, 60, and so on.
- Multiples of 12: 12, 24, 36, 48, 60, 72, and so on.
- Multiples of 15: 15, 30, 45, 60, 75, 90, and so on.
Since 60 is the least common multiple of all the multiples of three numbers, Therefore, the LCM of 10, 12, and 15 is 60, which can be written as follows:
LCM(10, 12, 15) = 60
Ladder Method
This method of determining LCM is undeniably popular. It is also the easiest way to find out the LCM of two or more than two numbers. So, here is a step-by-step solution for finding the LCM of 10, 12, and 15 using the ladder method:
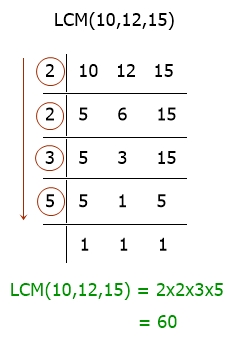
I hope you are familiar with the above method. If you're not, then here are some main steps:
- List out all the numbers.
- Divide the number by least to greatest (which equals the number) until the quotient is all one.
- That is, start with 2
- Check if 2 divides any of the given numbers.
- If it divides, then proceed and write down the quotient of the number (divided by 2) in the second line.
- Otherwise, check if 3 divides any of the given numbers.
- If it divides, then proceed. Otherwise, move on to the next one.
- Here, the quotient of the number (if it gets divided) will be written in the next line, and the rest of the number will be written as it is.
- Continue in this manner until every quotient equals 1.
Programs on LCM of numbers in different languages
« CodesCracker.com Next Topic »