Matrix Multiplication Rules and Formula

In this tutorial, you will learn all about matrix multiplication. Here I've shown the steps involved in matrix multiplication through pictorial representation. And I believe that pictorial representation is the best way to define any minorly complex topics. As a result, here are the two topics you should be aware of:

What the matrix is
How matrix multiplication works

I'll explain these two topics in terms that any programmer can understand.

What is the matrix?

In the programming world, a matrix is basically a two-dimensional (2D) array. Here "two dimension" means the element of an array arranged in two dimensions, which are rows and columns. Rows are from top-to-bottom, whereas columns are from left-to-right. For example,

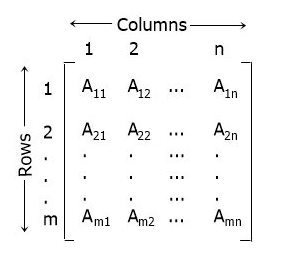
As you can see from the above matrix, there are a total of m numbers of rows and n numbers of columns. And A₁₁, A₁₂, ....., A_mn are matrix elements arranged in such a way that the element

A₁₁ is in the 1^st row and 1^st column
A₁₂ is in the 1^st row and 2^nd column
A_1n is in the 1^st row and n^th column
A₂₁ is in the 2^nd row and 1^st column
A₂₂ is in the 2^nd row and 2^nd column
A_2n is in the 2^nd row and n^th column
A_m1 is in the m^th row and 1^st column
A_m2 is in the m^th row and 2^nd column
A_mn is in the m^th row and n^th column

How matrix multiplication works

To multiply any two matrices, we need to do the dot product of the rows and columns. Before going to the step-by-step process of matrix multiplication, Let's first understand the matrix dot product. So to do the dot product of (1, 2, 3).(4, 5, 6). Here are the steps:

(1,2,3).(4,5,6)
= (1x4)+(2x5)+(3x6)
= 4+10+18
= 32

Now let's understand matrix multiplication using the step-by-step process given below.

Matrix Multiplication Procedure in Steps

Here is the step-by-step process to multiply the two given matrices:

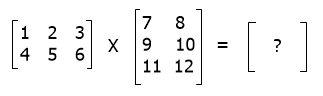
In the first step, perform the dot product of the first row's elements (of the first matrix) to the first column's elements (of the second matrix), as shown below:

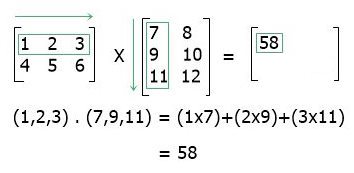
In the second step, perform the dot product of the first row's elements (of the first matrix) to the second column's elements (of the second matrix) as shown below:

In the third step, perform the dot product of the elements in the second row (of the first matrix) on the elements in the first column (of the second matrix), as shown below:

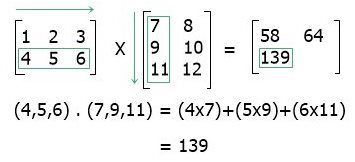
In the fourth step, perform the dot product of the second row's elements (of the first matrix) on the second column's elements (of the second matrix) as shown below:

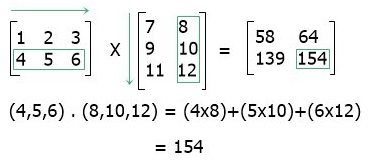
In this way, you can perform matrix multiplication.

Condition for matrix multiplication to be performed

In order for matrix multiplication to be performed or defined, the number of columns in the first matrix must be equal to the number of rows in the second matrix.

Further Explanation of Matrix Multiplication

The binary process known as "matrix multiplication" creates a matrix from two matrices. The first matrix's columns must have the same number of rows as the next matrix's rows in order for matrices to be multiplied.

The number of rows in the first matrix and the number of columns in the secondary matrix are added together to form the final matrix, or matrix product. The letters AB stand for the result of the matrices A and B. Thus, matrix multiplication is a fundamental tool of linear algebra and already has various uses in many branches of pure and practical arithmetic, including in statistics, physics, economics, and engineering.

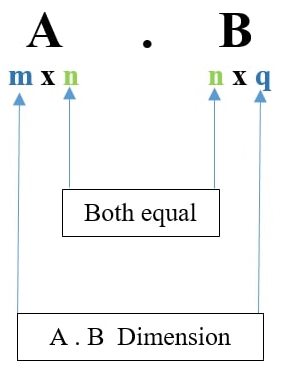
Assuming we possess two matrices A and B, matrix A may be multiplied by matrix B using the formula (AB). To put it another way, the resulting matrix for multiplying any m x n matrix "A" with a n x q matrix "B" may be expressed as matrix "C" of order m x q.

We can understand the general procedure of matrix multiplying by using the concept that "initial rows were multiplied with columns (component by component), and then all rows were completely filled."To multiply a matrix, use one of the following basic methods:
Step one is ensuring that the number of rows inside the second matrix matches the number of columns within the first matrix.

Step two involves multiplying the components of the i^th row of the first matrix by the components of the j^th column of the other matrix and then adding the results. That would be the component of the resulting matrix, which is under the i^th row as well as the j^th column.

Phase 3 is setting up the additional goods in their proper locations.

Multiplication of 2x2 Matrix

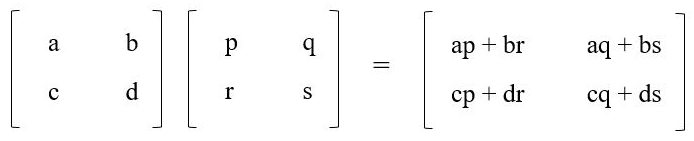
Multiplication of 3x3 Matrix

Example of Matrix Multiplication

Find the multiplication of A and B matrices. The matrix A =

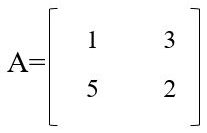
The Matrix B =

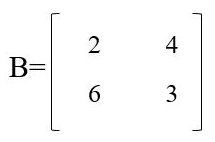
Therefore, A.B =

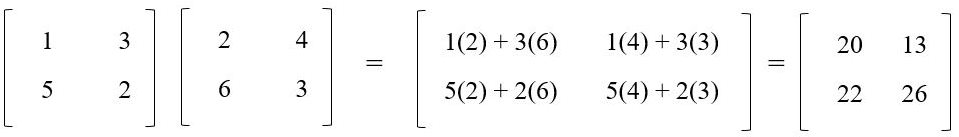
Programs created for matrix multiplication

« Previous Topic Next Topic »

Liked this post? Share it!