How to Add Two Matrices

This article was written and distributed with the intention of describing the process by which two matrices are added together. So without further ado, let's get right down to defining what exactly we mean when we say "matrix."

What is a matrix?

A matrix is the term used to refer to a collection of numbers that are laid out in the format of rows and column rows. For example:

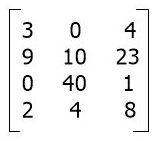
The matrix that was just shown has four rows, and each row has three columns. As a result, there is a total of 12 different elements or numbers that can be chosen from within this matrix. Let's get down to business and talk about the meat of the issue, which is the addition of two matrices or the process of adding matrices together.

Matrix addition

Let me explain the one necessary condition that must be met before we can proceed with the matrix addition. This condition is required in order for the matrix addition to take place. In addition, the requirement is that both matrices have an identical number of rows and columns.

Now is the time to set an example. Let's suppose there are two given matrices, matrix A and matrix B. The value of Matrix A is:

1  2
3  4

And the value of Matrix B is:

5  6
7  8

Then its addition goes like this:

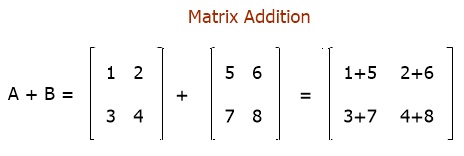
So we have another matrix, matrix C. The value of matrix C is:

6   8
10  12

This is the addition of two given matrices, A and B.

Further Explanation on Matrix Addition

As already said, for the matrix addition, there should be an equal number of rows and columns. In mathematics, adding two matrices involves adding the matching entries from each matrix. However, other operations, including the direct sum and the Kronecker sum, might also be regarded as addition for matrices.

Given A and B matrices as follows, find A+B. That is, the matrix A =

and the matrix B =

The total can be found by adding the elements from matrices A and B that are the same:

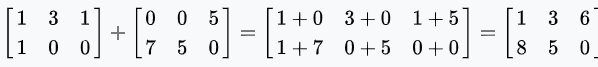
Programs created with matrix addition

« Previous Topic Next Topic »

Liked this post? Share it!