Formula to Find the Area and Perimeter of a Triangle

You are going to learn how to calculate the area and perimeter of a triangle by making use of the formulas that are provided in this article.

In contrast to the square and the rectangle, there are three distinct shapes that make up the triangle. As a direct consequence of this, all of the applicable formulas for various kinds and configurations of triangles are presented in this article.

The following are the two subjects that are discussed throughout this article:

• Area of the Triangle Formula
• Perimeter of the Triangle formula

Let's get right down to business and discuss the aforementioned two subjects, starting with the "area of the triangle formula" as soon as possible.

Area of the Triangle Formula

If the base and height of a triangle are given, then we will use the basic formula. Otherwise, if instead of base and height, the length of the three sides of a triangle is given, then we will approach "Heron's formula" to do the same job. Therefore, this section is divided into the following two sub-sections:

• Basic formula to find the area of a triangle
• Heron's formula to find the area of a triangle

Basic formula to find the area of a triangle

To find the area of a triangle based on its base and height values, use the following formula:

area = 1/2*b*h

The letters b and h represent the triangle's base and height, respectively. The above formula can also be written as:

area = 0.5*b*h

The figure given below shows the position of the base and height of a triangle:

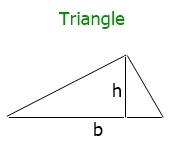
Note: Here h (height) is a perpendicular line to the base.

Heron's formula to find the area of a triangle

Heron's formula is used to find the area of a triangle using its three side lengths. Here is the formula:

area = square root of (s*(s-a)*(s-b)*(s-c))

The letters a, b, and c represent the triangle's three side lengths. And the value of s can be calculated as:

s = (a+b+c)/2

Perimeter of the Triangle formula

If the lengths of all three sides are not equal, then it is a scalene triangle. The scalene triangle looks like this:

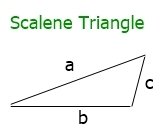
Therefore, here is the formula to find the perimeter of a Scalene triangle:

perimeter = a+b+c

The lengths of the three sides of a triangle are represented by a, b, and c.

And if the lengths of the two sides are equal, then it is an isosceles triangle. An isosceles triangle looks like this:

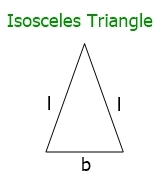
Therefore, here is the formula to find the perimeter of an isosceles triangle:

perimeter = (2*a)+b

Here, a indicates the length of a side (for equal ones) and b indicates the length of a side (for an unequal one).

And if all three sides are of equal length, then it is an equilateral triangle. An equilateral triangle looks like this:

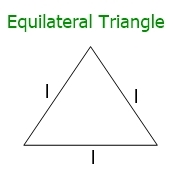
Therefore, here is the formula to find the perimeter of an equilateral triangle:

perimeter = 3*a

Here a indicates the length of any side of the triangle.