C Binary Tree

Binary trees are special trees because, when sorted, they lend themselves to rapid searches, insertions, and deletions. Since each item in a tree consists of information along with a link to the left member and a link to the right member, Here, this figure shows a small tree.

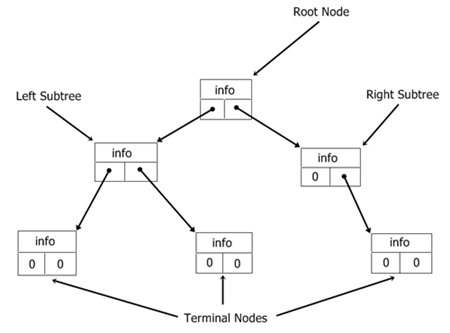
The "root" is the initial node in a tree. Each item is referred to as a "node" of the tree, and any part of the tree is referred to as a "subtree." A node with no subtrees attached to it is referred to as a "terminal node" or "leaf." The height of the tree is proportional to the number of layers deep its roots grow.

NoteA tree is simply a method for storing information in a logical manner in the memory, which is linear.

The binary tree is a type of linked list. Items can be added, removed, or accessed in any order.

Because the tree is a recursive data structure, most functions that use it are recursive. That is, each subtree is a tree in and of itself.

The order of a tree is determined by how it will be accessed. A "tree traversal" is the process of accessing each node in a tree. Consider the following tree:

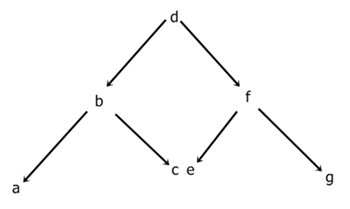
There are the following three ways to traverse a tree:

inorder: using inorder, you visit the left subtree, the root, and then the right subtree.
preorder: using preorder, you visit the root, the subtree, and then the right subtree.
postorder: using postorder, you visit the left subtree, the right subtree, and then the root.

Using each method, the order of access for the tree is shown here:

inorder: a b c d e f g
preorder: d b a c f e g
postorder: a c b e g f d

Even though a tree need not be sorted, most uses require this. Of course, what constitutes a sorted tree depends on how you will be traversing the tree.

The following function, stree(), builds a sorted binary tree:

struct tree
{
   char info;
   struct tree *left;
   struct tree *right;
};

struct tree *stree(struct tree *root, struct tree *r, char info)
{
   if (!r)
   {
      r = (struct tree *)
          malloc(sizeof(struct tree));
      if (!r)
      {
         printf("Out of Memory.\n");
         exit(1);
      }
      r->left = NULL;
      r->right = NULL;
      r->info = info;
      if (!root)
         return r;         // first entry
      if (info < root->info)
         root->left = r;
      else
         root->right = r;
      return r;
   }
   if (info < r->info)
      stree(r, r->left, info);
   else
      stree(r, r->right, info);
   return root;
}

C Binary Tree Example

Here is the complete example demonstrating a binary tree in C. This program constructs a binary tree in the C language.

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

#define ARRAY_SIZE 10

struct node
{
   char d;
   struct node *left;
   struct node *right;
};

typedef struct node NODE;
typedef NODE *BINARY_TREE;

BINARY_TREE newnode(void);
BINARY_TREE init_node(char d, BINARY_TREE p1, BINARY_TREE p2);
BINARY_TREE create_tree(char a[], int i, int size);
void preorder(BINARY_TREE root);
void inorder(BINARY_TREE root);
void postorder(BINARY_TREE root);

int main()
{
   char arr[ARRAY_SIZE];
   BINARY_TREE root;
   int lop;

   printf("Enter %d characters: ", ARRAY_SIZE);
   for (lop = 0; lop < ARRAY_SIZE; lop++)
   {
      scanf("%c", &arr[lop]);
      fflush(stdin);
   }
   root = create_tree(arr, 0, ARRAY_SIZE);
   assert(root != NULL);
   printf("\n");
   printf("Inorder:\t");
   inorder(root);
   printf("\n");
   printf("Preorder:\t");
   preorder(root);
   printf("\n");
   printf("Postorder:\t");
   postorder(root);
   printf("\n");

   return 0;
}

BINARY_TREE new_node()
{
   return ((BINARY_TREE)malloc(sizeof(NODE)));
}

BINARY_TREE init_node(char d1, BINARY_TREE p1, BINARY_TREE p2)
{
   BINARY_TREE temp;

   temp = new_node();
   temp->d = d1;
   temp->left = p1;
   temp->right = p2;
   return temp;
}

BINARY_TREE create_tree(char a[], int i, int size)
{
   if (i >= size)
   {
      return NULL;
   }
   else
   {
      return (init_node(a[i], create_tree(a, 2 * i + 1, size), create_tree(a, 2 * i + 2, size)));
   }
}

void preorder(BINARY_TREE root)
{
   if (root != NULL)
   {
      printf("%c ", root->d);
      preorder(root->left);
      preorder(root->right);
   }
}

void inorder(BINARY_TREE root)
{
   if (root != NULL)
   {
      inorder(root->left);
      printf("%c ", root->d);
      inorder(root->right);
   }
}

void postorder(BINARY_TREE root)
{
   if (root != NULL)
   {
      postorder(root->left);
      postorder(root->right);
      printf("%c ", root->d);
   }
}

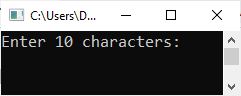
The following snapshot shows the initial output produced by the above program:

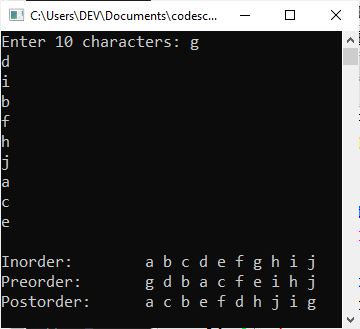
Now supply 10 characters as input in such a way that you first type a character, say "g," and hit the ENTER key, then type the second character, say "d," and hit the ENTER key, and so on. Here is the sample output after supplying ten character inputs: g, d, i, b, f, h, j, a, c, and e.