Why NAND and NOR gates are called universal gates

The purpose of writing and publishing this article was to provide an answer to the following question: "Why are NAND and NOR gates sometimes referred to as universal gates?"

This article is broken up into two parts, which are as follows:

• Why is the NAND gate referred to as a universal gate?
• Why is the NOR gate referred to as a universal gate?

But before we get started, let's make sure we have a firm grasp on what the term "universal gate" actually refers to.

What is universal gate?

The universal gate is the gate that allows all basic gates to be formed.

As we all know, an AND gate followed by a NOT gate makes a NAND gate. And the NAND gate is universal only because all of the other basic gates—the OR gate, the AND gate, and the NOT gate—can be easily designed from it.

Now let's start proving how NAND and NOR gates are referred to as universal gates, starting with the "NAND" gate.

Why is the NAND gate referred to as a universal gate?

In this part of the article, I will demonstrate why a NAND gate is often referred to as a "universal gate." Let's look at how basic gates are built from the NAND gate.

Using a NAND gate as a NOT gate

The symbol below depicts the construction of a NOT gate using a NAND gate.

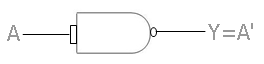
Here, A is the input, and Y is the output that will be equal to A' or A̅. If A is the input and A̅ is the output, which is the reverse of A, Therefore, this gate is working like a NOT gate.

AND gate using a NAND gate

To design an AND gate using NAND gates, we have to use two NAND gates as shown in the figure below:

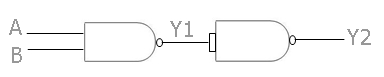
As you can see from the above figure, in the first NAND gate, there are two inputs, A and B, which give one output, Y1, that is equal to (A.B)' or A.B. Now in the second NAND gate, the Y1 is an input that gives the Y2 as an output that is equal to ((A.B)')'. And as we know, if we double complement any number, the original or natural number will be obtained, that is, (A.B) and it will be the final output produced from the second NAND gate.

Therefore, the initial conclusion is that we have provided two inputs, A and B, and have gotten the output (A.B). This works in the same way as the AND gate.

OR gate using a NAND gate

To make an OR gate using NAND gates, we have to apply three NAND gates as shown in the following figure:

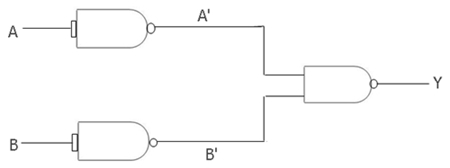
As you can see, the first NAND gate has A as an input, which becomes A' at the output.And from the second NAND gate, we have B as an input that becomes B' at the output. We now have two inputs (A' and B') that output Y at the third NAND gate. And Y contains (A'.B')'.

By using De Morgan's second theorem, that is:

(A.B)' = A'+B'

Therefore, by applying the above theorem to the output, which is (A'.B')', we get:

(A'.B')' = (A')' + (B')'

And as we also know, when we double complement the number, we will get the same number but in uncomplemented form. Therefore, the above equation becomes:

(A'.B')' = A + B

Now the conclusion is, we have two inputs, A and B, as seen from the above figure, and we have one output that contains A+B. And this works the same as the OR gate works, so we have successfully made the OR gate using the NAND gate.

Conclusion about the NAND gate as a universal gate

As you can see here, we have made all three basic gates, that is, the AND, OR, and NOT gates, using the NAND gate. Therefore, the NAND gate is called a universal gate.

Why is the NOR gate referred to as a universal gate?

In this part of the article, I will demonstrate why a NOR gate is often referred to as a "universal gate."

As we all know, an OR gate followed by a NOT gate makes a NOR gate. And because it can be used to design all of the basic gates (the AND gate, the OR gate, and the NOT gate), it is classified as a universal gate.

Now let's design all three basic gates through the NOR gate to identify it as a universal gate.

NOT gate using a NOR gate

Here is the figure that shows how to design a NOT gate using a NOR gate:

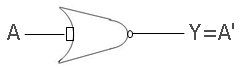
Here, input A becomes output A'. As a result, it functions similarly to a NOT gate.

OR gate using a NOR gate

To design an OR gate using a NOR gate, we have to use two NOR gates. Concentrate on the following figure:

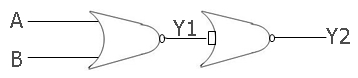
In this case, the first NOR gate's inputs are A and B, and the output is Y1, which equals (A + B)'. And the input at the second NOR gate is Y1 or (A+B)', which produces Y2 at output, and Y2 is equal to ((A+B)')'. If we double complement any number, then the same number or the number in uncomplemented form will be obtained. Therefore, the final output will be A+B.

And if we have two inputs (A and B) that produce A+B at the output, then this works the same as an OR gate. It means we have successfully designed or constructed an OR gate using a NOR gate.

AND gate using a NOR gate

We have to take the help of three NOR gates to design it in such a way that it takes input and produces output in the same way the AND gate takes and produces. Therefore, here is the figure that says everything about designing an AND gate using a NOR gate:

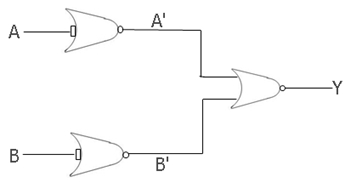
In this case, the first NOR gate's input is A, and the output is A'. And the second NOR gate's input is B, which results in B' at the output. And the third NOR gate's two inputs are A' and B', resulting in Y as the output, which is equal to (A' + B')'.

By De Morgan's first theorem:

(A+B)' = A'.B'

Therefore, by applying the above De Morgan theorem to the expression (A'+B')' which is at the final output in the above figure:

(A'+B')' = (A')'.(B')'

can be simplified as

(A'+B')' = (A.B)

Now, in this case, the two inputs are A and B, which give the final output A.B that works the same as the AND gate does. Therefore, we have successfully designed an AND gate using a NOR gate.

Final thoughts on the NOR gate as a universal gate

As you can see here, we have successfully designed all three basic gates—AND, OR, and NOT—through the NOR gate; therefore, the NOR gate can be called a universal gate.

Computer Fundamentals Quiz