- Digital Electronics Course
- Digital Electronics Tutorial
- Logic Gates
- NAND NOR as a Universal Gate
- Boolean Algebra
- Proof of Theorems and Postulates
- De-Morgan's Theorems
- Duality Principle
- Sum of Products (SOP)
- Product of Sum (POS)
- Canonical SOP Form
- Canonical POS Form
- SOP to Standard SOP
- POS to Standard POS
- Standard SOP to Minimal SOP
- Standard POS to Minimal POS
- Computer Programming
- Learn Python
- Python Keywords
- Python Built-in Functions
- Python Examples
- Learn C++
- C++ Examples
- Learn C
- C Examples
- Learn Java
- Java Examples
- Learn C#
- Learn Objective-C
- Web Development
- Learn HTML
- Learn CSS
- Learn JavaScript
- JavaScript Examples
- Learn SQL
- Learn PHP
De Morgan's Theorem of Boolean Algebra
There are two theorems given by De Morgan's for boolean algebra that we are going to discuss in this article or tutorial.
De Morgan's First Theorem
De Morgan's first theorem states that the complement of the sum equals the product of the complement.
Boolean Expression of De Morgan's First Theorem
Here is the boolean expression of De Morgan's first theorem:
(A+B)' = (A'.B')
Here, A and B are the two binary variables. Binary variables are those in which both variables can hold either 0 or 1.
Graphical Representation of De Morgan's First Theorem
Below is the symbol or graphical representation of De Morgan's first theorem:
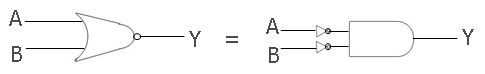
As you can see from the above figure, the first gate is a NOR gate, which is taking two inputs, A and B, and giving the output Y that will be equal to (A+B)'. And the second gate is the AND gate, but here there are two inputs A and B that are passing through a NOT gate and then enter the AND gate as input. Therefore, at the AND gate's input terminal, both the inputs will become A' and B', and therefore the output Y holds the value (A'.B').
Proof of De Morgan's First Theorem using the Truth Table
Here is the truth table that identifies the proof of De Morgan's first theorem equation, which is (A+B)'=(A'.B'):
| A | B | A' | B' | A+B | (A+B)' | A'.B' |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
As you can clearly see, all the corresponding row's values of (A+B)' and (A'.B') are same. Therefore, the first theorem of De Morgan is proved using the above truth table.
De Morgan's Second Theorem
According to De Morgan's second theorem, the complement of produce equals the sum of the complement.
Boolean Expression of De Morgan's Second Theorem
The boolean expression of De Morgan's second theorem is given below:
(A.B)' = (A'+B')
Graphical Representation of De Morgan's Second Theorem
Here is the symbol or graphical representation of the second theorem given by De-Morgan:
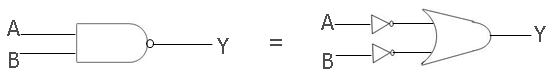
Here, the first gate is a NAND gate; there are two inputs, A and B, provided here, which give Y at the output and will be equal to (A.B)'. And the second gate is an OR gate, and the inputs A and B provided here are passed through a NOT gate; therefore, these two inputs become A' and B' at output, which will be the input for the OR gate that gives Y at output that will be equal to (A'+B').
Proof of De Morgan's Second Theorem using Truth Table
Here is the truth table to demonstrate De Morgan's second theorem:
| A | B | A' | B' | A.B | (A.B)' | A'+B' |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
Again, as you can see, (A.B)' holds the same value as (A'+B') holds in all corresponding rows. Therefore, De Morgan's second theorem is demonstrated using the above truth table.
« Previous Tutorial Next Tutorial »